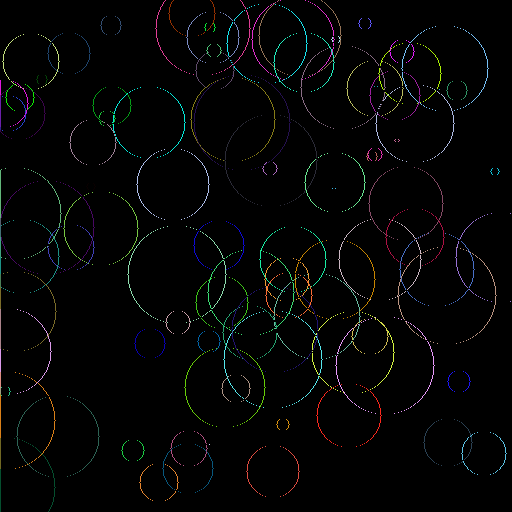Drawing circles
As part of my PhD research I had to implement discrete Sibson interpolation , to do some nifty interpolation. Sibson interpolation is a scheme based on areas of Voroni regions which can be quite complex. But for the discrete case Park et al presents a nice and simple scheme.
- For each pixel find the nearest neighbor ( of the points you are interpolating between)
- Draw a circle with radius = distance(this, nearest neighbor)
- Normalize, divide each raster color with the number of circles that contributed.
The first, and very importantly functional, implementation of the circle drawing routine was a simple double loop. It worked, but it nagged me that it was slow and it seemed like a fun problem. So I went home an wrote a small program to draw circles and test the speed. The top image show such a case.
You can find the code on github: https://github.com/jtpedersen/draw-circles
I made a small test framework just to have some fun trying to optimize the drawing. The authors of the paper use a shader and somewhat similar to this transforms each point into a quad and only draws within the circle. I needed to do it on CPU for now.
Drawing 512^2 random circles in this manner takes my laptop around 10 seconds. It is obviously to slow and inefficient. The method it self is not good, as it access the same pixels multiple times to addColor. So the first trick was to turn it in to a two-stage algorithm. First note where each circle starts and ends on each row. Now the central loop does not depend on the area but the circumference of the circle. The second stage is scanning through the temporary buffer and accumulating the results.
To calculate the start and end point we scan the y axis and for each row we determine the x-offset. The formula for the circle is (x – x0)^2 + (y-yo)^2 = r^2. We can assume x0 and y0 is zero, the circle is centered at (0,0) for the calculation and then do the offset calculation afterwards. Since we now y we just have to solve for x, diff = sqrt(r^2-x^2). In the extra buffer we then store color at (y, xo -diff) and -color ar (y, xo+diff+1), so scanning is adding the value in the extra buffer into an accumulator and writing it into the same place in output buffer. I also made a version with two extra buffers, one for enterPixel the other for exit, but this is not necessary.
Even though this is a two-stage algorithm it is much faster. It is down to 655 msec. For the case with 512^2 random circles. It is worth noting that the radius of the circles is restricted to 10% of the width of the image, as this seemed like a fairly large value, yet still realistic.
I could not come up with a better algorithm, maybe you can?
A little complexity analysis. Assume that worst case is all circles have a radius that is so large that we have to paint all pixels in a n*n grid. The naive version will then for m updates do m * n^2 and the smarter version will only do m * 2 *n + n^2 work. if we assume that m ~ n^2 we have that the naive algorithm runs in O(n^2 * n^2) = O(n^4) and the smart in just O( n^2 * 2 * n + n^2) = O(n^3).
Since I ran out of good ideas I went for the next best thing, trying to optimize. This would be the ideal time to start a profiler, I like Kcachegrind. But i had inserted timings and an idea of a culprit, the square root. So I did the next best thing commented the line out and observed the incredible speed up. Down to 200 msec. However we still have to calculate the value.
There are clever algorithms for integer square root, but I did have the advantage of knowing the range and that it was rather small. All values would be less than the largest radius^2, for these test cases that would be < (512 * .1)^2 = 2621.4< 2^13 = 8192. So the simple thing to try was to use a lookup table low and behold we are up to 277 msec but we actually calculate the right value.
Since memory access is always best to do in order and the randomness of the input really destroys locality, i thought that it could be interesting to see what would happen if the points were in order. So as i quick hack i sorted the points based on the y coordinate of the center of the circles. This cut off another 100 msecs and yet sorting took only 20 msecs, so a net gain of 80 msecs. (for the interpolation case the input will actually be sorted)
This is where i stopped, but what should be the next step? I compile with gcc and use -O3. I quick look at the assembly shows that gcc uses sse instructions, but this could perhaps be pursued? I initially thought that i could get a speed up from scanning in parallel, but my timings says that scanning only takes few msecs. I would like to parallelize the setting the values, but it is not as trivial as there are obvious concurrency issues. Maybe just a mutex pr row and everything would be fine.
Anyhow down from 10 secs to just shy of .2 sec is quite alright in my book. Could it be improved? What would be the next step? generate all events (start /stop) put them in a list, sort and scan through this instead of a n*n buffer?